RATest. A Randomization Tests package is available on CRAN
This blog post introduces the RATest package we released a while back on CRAN with my colleague and good friend Mauricio Olivares-Gonzalez. The package contains a collection of randomization tests, data sets and examples. The current version focuses on two testing problems and their implementation in empirical work, mostly related to economics. First, it facilitates the empirical researcher to test for particular hypotheses, such as comparisons of means, medians, and variances from k populations using robust permutation tests, which asymptotic validity holds under very weak assumptions, while retaining the exact rejection probability in finite samples when the underlying distributions are identical. Second, it implements Canay and Kamat (2017) permutation test for testing the continuity assumption of the baseline covariates in the sharp regression discontinuity design (RDD).
In this post we’ll focus on the implementation of Canay and Kamat (2017) test presening a summarized version of the vignette that is available on CRAN. For those stata enthusiasts there is an implementation of this function in stata see RDPerm
Set up of the problem
One of the assumptions in which a Sharp Regression Discontinuity Design rests is that baseline covariates are continuous at the cutoff. However, this hypothesis of continuity is intrinsically intestable. Practitioners have relied on graphical inspections, or on conditional means tests, neither of which is a test for the continuity of the baseline covariates at the cutoff.[1]
Canay and Kamat (2017) propose a permutation test approach to test this hypothesis, where the null hypothesis states the continuity of the distribution of the baseline covariates at the cutoff. Permutation tests have several advantages in the testing problem we are concerned. They can be applied without parametric assumptions of the underlying distribution generating the data. They also can control the limiting rejection probability under general assumptions.
We organize this post like the vignette proceding in a similar but for succinct fashion.
Testable Hypothesis
Potential Outcomes
Consider the simplest model for a randomized experiment with subject i’s (continuous) response \(Y_i\) to a binary treatment \(A_i\). The treatment assignment in the sharp RDD follows the rule \(A_i=\{Z_i\ge\bar{z}\}\), where \(Z_i\) is the so called running variable, and \(\bar{z}\) is the cutoff at which the discontinuity arises. This threshold is conveniently assumed to be equal to 0.
For every subject \(i\), there are two mutually exclusive potential outcomes - either subject gets the treateatment or not. If subject i receives the treatment (\(A_i = 1\)), we will say the potential outcome is \(Y_i(1)\). Similarly, if subject i belongs to the control group (\(A_i = 0\)), the potential outcome is \(Y_i(0)\). We are interested in the average treatment effect (ATE) at the cutoff, i.e.
\[𝔼(Y_i(1)−Y_i(0)|Z = 0)\]The identification assumption is not testable nonetheless as we only get to observe at most one of the potential outcomes.[2] Lee (2008) established a more restrictive but testable sufficient condition for identification - units can control the running variable except around the cutoff.[3] The identifying assumption implies that the baseline covariates are continuously distributed at the cutoff
\[H(w|z)z=0 \,\,for \, all \,\, W \in 𝒲 \,\,\,\, (1)\]where \(W\in\mathcal{W}\) denotes the baseline covariates. We can cast condition (1) in terms of a two-sample hypothesis testing problem. Let
\[H^− (w|0)=\underset{z\uparrow0}{lim} H(w|0) \,\,and \,\, H^+ (w|0)=\underset{z\downarrow0}{lim} H(w|0)\]Condition (1) is equivalent to \(H(w\vert z)\) being right continuous at \(z=0\) and
\[H^− (w|0)=H^+ (w|0) \,\,for \, all \,\, W \in 𝒲 \,\,\,\, (2)\]Therefore, testing the null hypothesis of continuity of the baseline covariates at the cutoff \(Z = 0\) reduces to testing for condition (2).
Induced Order Statistics
Consider a random sample \(X^{(n)} = {(Y_i ^*, W_i, Z_i)}_{i = 1}^n\) from a distribution \(P\) of \((Y^*, W, Z)\). The order statistics of the sample of the running variable, \(Z_{(1)}\leq Z_{(2)}\leq ... \leq Z_{(n)}\) will in sample of the baseline covariate, say, \(W_{[1]}\leq W_{[2]}\leq ... \leq W_{[n]}\) according to the rule: if \(Z_{(j)}= Z_k\) then \(W_{[j]} = W_k\) for all \(k = 1, ..., n\). It is worth mentioning that the values of this induced order statistics are not necessarily ordered.
The test statistic
The test statistic exploits the behavior of the closest units to the left and right of the cutoff \(\bar{z}=0\). More precisely, fix q ∈ ℕ and take the q closest values of the order statistics of \({Z_i}\) to the right, and the \(q\) closest values to the left:
\[Z_{(q)}^-, Z_{(q-1)}^-,...,Z_{(1)}^-\]and
\[Z_{(1)}^+, Z_{(2)}^+,...,Z_{(q)}^+\]respectively. The induced order for the baseline covariates is then
\[W_{[q]}^-, W_{[q-1]}^-,...,W_{[1]}^-\]and
\[W_{[1]}^+, W_{[2]}^+,...,W_{[q]}^+\]respectively. The random variabes \({W_{[q]}^-, W_{[q-1]}^-,...,W_{[1]}^-}\) can be viewed as an independent sample of \(W\) conditional on \(Z\) being close to the cutoff from the left. Analogously, \({W_{[1]}^+, W_{[2]}^+,...,W_{[q]}^+}\) can be thought of an independent sample of \($W\)$ conditional on \($Z\)$ being close to the cutoff from the right. Let \(H_n^−(w)\) and \(H_n^+(w)\) be the empirical CDFs of the two samples of size \(q\), respectively,
\[H^-_n(w)=\frac{1}{q}\sum_{i=1}^q I\{W^{-}_{[i]}\le w\}\]and
\[H^+_n(w)=\frac{1}{q}\sum_{i=1}^q I\{W^{+}_{[i]}\le w\}\]Stack all the \(2q\) observations of the baseline covariates into
\[S_n=(S_{n,1},\dots,S_{n,2q})=(W^{-}_{[1]}, \dots, W^{-}_{[q]},W^{+}_{[1]},\dots, W^{+}_{[q]})\]The test statistic is a Cramér-von Mises type test:
\[T(S_n)=\frac{1}{2q}\sum_{i=1}^{2q}\left(H^-_n(S_{n,i})-H^+_n(S_{n,i})\right)^2\]Computing p-values
We argued that the permutation test rejects the null hypothesis (2) if \(T(S_n)\) is bigger than the \(1 − \alpha\) quantile of the randimization distribution. Alternatively, we can define the p-value of a permutation test, \(\hat{p}\), as
\[\hat{p}=\frac{1}{N}\sum_{\pi\in \mathbf{G}_{2q}}I\{T(S_{n,\pi(1)},\dots,S_{n,\pi(2q)})\ge T(S_{n})\}\]where \(T(S_n)=T(S_{n,1},\dots,S_{n,2q})\) is the observed sample, and \(N\) is the cardinality of \(\mathbf{G}_N\). It can be shown
\[P(\hat{p}\le u)\le u\:\:\:\text{ for all }\] \[\:\:\:0\le u \le1,\:\:\] \[P\in\mathbf{P}_0\]therefore, the test that rejects when \(\hat{p}\le \alpha\) is level \(\alpha\).
Stochastic approximation
When computing the permutation distribution, we often encounter the situation that the cardinality of \(\mathbf{G}_{2q}\) might be large such that it becomes computationally prohibitive. In this situation, it is possible to approximate the \(p\)-values the following way. Randomly sample permutations \(\pi\) from \(\mathbf{G}_{2q}\) with or without replacement. Suppose the sampling is with replacement, then \(\pi_1,\dots,\pi_N\) are i.i.d. and uniformly distributed on \(\mathbf{G}_{2q}\). Then
\[\tilde{p}=\frac{1}{B}\left(1+\sum_{i=1}^{B-1}I\{T(S_{n,\pi_i(1)},\dots,S_{n,\pi_i(2q)})\ge T(S_{n})\}\right)\]is such that
\[P(\tilde{p}\le u)\le u\:\:\:\text{ for all }\:\:\:0\le u \le1,\:\: P\in\mathbf{P}_0\]where this $P$ takes into account the randomness of \(T(\cdot)\) and the sampling of the \(\pi_i\). Like in the previous case, the test that rejects when \(\tilde{p}\le \alpha\) is level \(\alpha\).
It is worth noticing that the approximation \(\tilde{p}\) satisfies the above equation regardless of \(B\), although a bigger \(B\) will improve the approximation. As a matter of fact, \(\tilde{p}-\hat{p}=o_p(1)\) as \(B\to\infty\). The RATest package uses \(B=499\) by default.
Tuning parameter q
The implementation of the test statistic heavily relies on \(q\), the number of closest values of the running variable to the left and right of the cutoff. This quantity is small relative to the sample size \(n\), and remains fixed as \(n\to\infty\). Canay and Kamat (2017) recomend the rule of thumb
\[q=\left\lceil f(0)\sigma_Z\sqrt{10*(1-\rho^2)}\frac{n^{3/4}}{\log n} \right\rceil\]where \(\lceil\nu\rceil\) is the smallest integer greater or equal to \(\nu\), \(f(0)\) is the density if \(Z\) at zero, \(\rho\) is the coefficient of correlation \(W\) and \(Z\), and \(\sigma^2_Z\) is the variance of \(Z\). For the scalar case, it can be estimated from sample. The feasible tuning parameter is
\[\hat{q}=\left\lceil \max\left\{\min\left\{\hat{f}_n(0)\hat{\sigma}_{n,z}\sqrt{10*(1-\hat{\rho}^2_n)}\frac{n^{3/4}}{\log n}, q_{UB}\right\},q_{LB}\right\} \right\rceil\]where \(q_{LB}=10\), and \(q_{UB}=n^{0.9}/\log n\). The lower bound, \(q_{LB}\) represents situations in which the randomized and non-randomized versions of the permutation test differ, whereas the upper bound, \(q_{UB}\) guarantees the rate of convergence does not violate the formal results in Canay and Kamat (2017), theorem 4.1. The same reasoning applies if we replace \(q\) with \(q^a\). The density function \(\hat{f}_n(\cdot)\) is estimated employing the univariate adaptative kernel density estimation à la Silverman (e.g. Portnoy and Koenker (1989), Koenker and Xiao (2002), Silverman (1986)}, and the results are obtained directly from the R package quantreg. Finally, \(\rho\) and \(\sigma_Z\) are estimated by their sample counterparts.
The RATest package also computes the corresponding rule of thumb that changes a little bit in when W is a K-dimensional vector, since the variances and correlations are not scalars.
Empirical Illustration
The empirical illustration is based on Lee’s (2008) of the effect of party incumbency advantage in electoral outcomes. For comparative purposes we follow the same empirical study chosen by Canay and Kamat (2017).
The objective of Lee’s (2008) is to assess whether a Democratic candidate of the US. House of Representative has an edge over his competitors if his party won the previous election. The causal effect of party incumbency is captured by exploiting the fact that an election winner is determined by \(D= 1(Z \geq 0)\) where \(Z\), the running variable, is the vote shares between Democrats and Republicans.
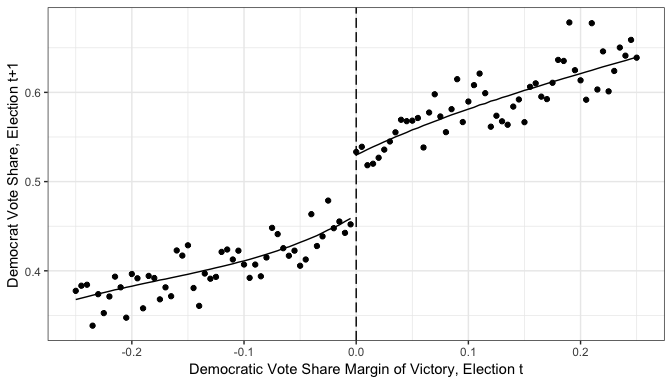
Figure 1 shows Lee (2008) sharp RD strategy. The figure illustrates the sharp change in probability of a Democrat winning against the difference in vote share in the previous election. The data used here and contained in the package have six covariates and 6,558 observations with information on the Democrat runner and the opposition. The data set is named , and it is a subset of the publicly available data set in the Mostly Harmless Econometrics Data Archive
#Load Package
require("RATest")
# Load the data set
lee2008<-lee2008
lee2008$d<- ifelse(lee2008$difdemshare >= 0,1,0)
# Predict with local polynomial logit of degree 4
logit.a <- glm(formula = demsharenext ~ poly(difdemshare, degree = 4) +
poly(difdemshare, degree = 4) * d,
family = binomial(link = "logit"),
data = lee2008)
lee2008$demsharenexthat<-predict(logit.a, lee2008, type = "response")
# Create local average by 0.005 interval of the running variable (share)
breaks <- round(seq(-1, 1, by = 0.005), 3)
lee2008$i005<-as.numeric(as.character(cut(lee2008$difdemshare,
breaks = breaks,
labels = head(breaks, -1),
right = TRUE)))
m_next<-tapply(lee2008$demsharenext,lee2008$i005,mean)
m_next<-data.frame(i005=rownames(m_next), m_next=m_next)
mp_next<-tapply(lee2008$demsharenexthat,lee2008$i005,mean)
mp_next<-data.frame(i005=rownames(mp_next), mp_next=mp_next)
panel.a<-merge(m_next,mp_next,by=c("i005"), all=T)
panel.a$i005<-as.numeric(as.character(panel.a$i005))
# Plot panel (a) MHE
panel.a <- panel.a[which(panel.a$i005 > -0.251 & panel.a$i005 < 0.251), ]
plot.a <- ggplot(data = panel.a, aes(x = i005)) +
geom_point(aes(y = m_next)) +
geom_line(aes(y = mp_next, group = i005 >= 0)) +
geom_vline(xintercept = 0, linetype = 'longdash') +
xlab('Democratic Vote Share Margin of Victory, Election t') +
ylab('Democrat Vote Share, Election t+1') +
theme_bw()
plot.a
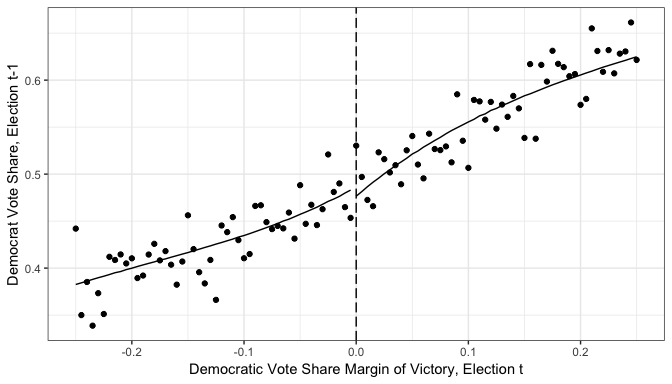
One check used by practitioners to assess the credibility of the RD designs relies on graphical depiction of the conditional mean of the baseline covariates . Figure 2 plots this for the Democrat vote share in \(t − 1\). A simple visual inspection would lead the researcher to conclude that there are no discontinuities at the cutoff for these baseline covariates.
# Predict with local polynomial logit of degree 4
logit.b <- glm(formula = demshareprev ~ poly(difdemshare, degree = 4) +
poly(difdemshare, degree = 4) * d,
family = binomial(link = "logit"),
data = lee2008)
lee2008$demshareprevhat<-predict(logit.b, lee2008, type = "response")
# Create local average by 0.005 interval of the running variable (share)
breaks <- round(seq(-1, 1, by = 0.005), 3)
lee2008$i005<-as.numeric(as.character(cut(lee2008$difdemshare,
breaks = breaks,
labels = head(breaks, -1),
right = TRUE)))
m_next<-tapply(lee2008$demshareprev,lee2008$i005,mean)
m_next<-data.frame(i005=rownames(m_next), m_next=m_next)
mp_next<-tapply(lee2008$demshareprevhat,lee2008$i005,mean)
mp_next<-data.frame(i005=rownames(mp_next), mp_next=mp_next)
panel.b<-merge(m_next,mp_next,by=c("i005"), all=T)
panel.b$i005<-as.numeric(as.character(panel.b$i005))
# Plot panel (b) MHE
panel.b <- panel.b[which(panel.b$i005 > -0.251 & panel.b$i005 < 0.251), ]
plot.b <- ggplot(data = panel.b, aes(x = i005)) +
geom_point(aes(y = m_next)) +
geom_line(aes(y = mp_next, group = i005 >= 0)) +
geom_vline(xintercept = 0, linetype = 'longdash') +
xlab('Democratic Vote Share Margin of Victory, Election t') +
ylab('Democrat Vote Share, Election t-1') +
theme_bw()
plot.b
This package however, implements Canay and Kamat (2017) in the function . The following code performs the test for the continuity of the named in the data set at the threshold. The function requires the name of the baseline covariate to be tested, the running variable , the data set name. We also specify a natural number that will define the q closest values of the order statistics of the running variable () to the right and to the left of the cutoff. As default, the function uses the Cram’er-von Mises test . The function is available for a concise summary of the result.
# Lee2008
set.seed(101)
permtest<-RDperm(W="demshareprev", z="difdemshare",data=lee2008,q_type=51)
summary(permtest)
#>
#> **********************************************************
#> ** RD Distribution Test using permutations **
#> **********************************************************
#> Running Variable: difdemshare
#> Cutoff: 0
#> q: Defined by User
#> Test Statistic: CvM
#> Number of Permutations: 499
#> Number of Obs: 6558
#>
#> **********************************************************
#> H0: 'Continuity of the baseline covariates at the cutoff'
#> **********************************************************
#>
#> Estimates:
#> T(Sn) Pr(>|z|) q
#> demshareprev 0.03 0.01 51 **
#> ---
#> Signif. codes: 0.01 '***' 0.05 '**' 0.1 '*'
The function reports the vaule of the test statistics (\(T(Sn)\)), the p-value and the number of q closest values used. This is particularly relevant when the user chooses any of the `rule of thumb’ methods for q. The function allows for multiple baseline covariates as well, in which case it will return the join test. The following code shows how to do this
permtest_rot<-RDperm(W=c("demshareprev","demwinprev", "demofficeexp"),
z="difdemshare",data=lee2008,q_type='rot', n.perm=600)
summary(permtest_rot)
#>
#> **********************************************************
#> ** RD Distribution Test using permutations **
#> **********************************************************
#> Running Variable: difdemshare
#> Cutoff: 0
#> q: Rule of Thumb
#> Test Statistic: CvM
#> Number of Permutations: 600
#> Number of Obs: 6558
#>
#> **********************************************************
#> H0: 'Continuity of the baseline covariates at the cutoff'
#> **********************************************************
#>
#> Estimates:
#> T(Sn) Pr(>|z|) q
#> demshareprev 0.08 0 32 ***
#> demwinprev 0.08 0 35 ***
#> demofficeexp 0.06 0.01 45 **
#> Joint.Test 0.11 0 32 ***
#> ---
#> Signif. codes: 0.01 '***' 0.05 '**' 0.1 '*'
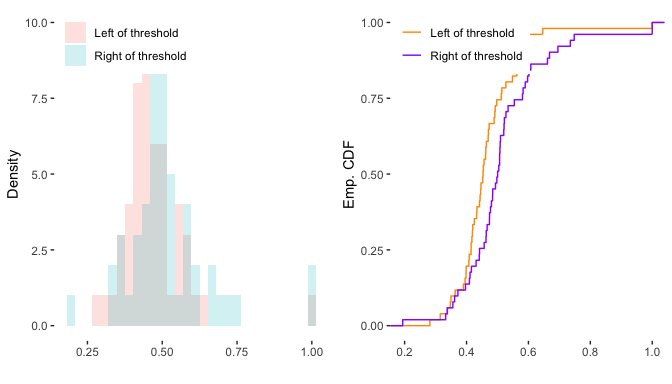
A plot function is also available for objects of the class RDperm. It works as the base function, but it needs the specification of the desired baseline covariate to be plotted. The output can be a ggplot histogram (hist), CDF (cdf) or both. The default is both.
plot(permtest,w="demshareprev")
Conclusions
In this blog post we described the RDperm funcion on the RATest package in R, which allows the practitioner to test the null hypothesis of continuity of the distribution of the baseline covariates in the RDD, as developed by Canay and Kamat (2017). Based on a result on induced order statistics, the RATest package implements a permutation test based on the Cramér-von Mises test statistic.
The main functionalities of the package have been illustrated by applying them to the celebrated RDD of the U.S. House elections in Lee(2008)
References
Canay, Ivan A, and Vishal Kamat. 2017. “Approximate Permutation Tests and Induced Order Statistics in the Regression Discontinuity Design.” The Review of Economic Studies 85 (3). Oxford University Press: 1577–1608.
Hahn, Jinyong, Petra Todd, and Wilbert Van der Klaauw. 2001. “Identification and Estimation of Treatment Effects with a Regression-Discontinuity Design.” Econometrica 69 (1). Wiley Online Library: 201–9.
Koenker, Roger, and Zhijie Xiao. 2002. “Inference on the Quantile Regression Process.” Econometrica 70 (4). Wiley Online Library: 1583–1612.
Lee, David S. 2008. “Randomized Experiments from Non-Random Selection in Us House Elections.” Journal of Econometrics 142 (2). Elsevier: 675–97.
Portnoy, Stephen, and Roger Koenker. 1989. “Adaptive L-Estimation for Linear Models.” The Annals of Statistics. JSTOR, 362–81.
Silverman, Bernard W. 1986. Density Estimation for Statistics and Data Analysis. Vol. 26. CRC press.
[1] This has been highlighted by Canay and Kamat (2017). See Appendix E for a survey of the topic in leading journals from 2011 to 2015.
[2] To put it in a more compact way, we say individual \(i\)’s observed outcome, \(Y^{*}_i\) is \(Y^{*}_i=Y_i(1)A_i+Y_i(0)(1-A_i)\), whereas the identification assumption in Hahn et al (2001) requires that both \(E(Y_i(1)\vert Z=z)\:\:\:\text{ and }\:\:\:E(Y_i(0)\vert Z=z)\:\text{ are continuous in }\:z\text{ at }\:0\)
[3] See condition 2b in Lee (2008).
Ignacio
Sarmiento Barbieri
University of Los Andes
- srmntbr2 (at) illinois.edu
- ignaciomsarmiento (at) gmail.com
- ignaciomsarmiento
Blogs/Links
These are blogs/sites I frequently visit