Mean and Quantile Regression using Mosek
Many of the problems we encounter in Econometrics can be formulated as a linear or a quadratic problem. In this post, I want to approach two traditional problems: Quantile Regression and Ordinary Least Squares as convex problems and how to implement them in R using the package RMosek.
There are many convex optimizer solvers available for R, a survey can be found at the CRAN Task View: Optimization and Mathematical Programming. But here, I want to center my attention on Rmosek (Friberg 2014). Rmosek is an interface that makes available Mosek from R and it’s available from CRAN. Mosek is an “optimization software designed to solve large-scale mathematical optimization problems” (Mosek, 2011). Probably one of Mosek’s greatest features is that nonlinear separable convex optimization problems can be easily implemented and solved.
I begin this post by writing the Quantile and Ordinary Least Squares problems in their linear and quadratic forms respectively. Outlined the analytic form, I write functions that implement them in Rmosek. Finally, I test my Rmosek function to benchmark R functions in a simulation exercise, and in a replication exercise. Overall, once the analytic forms of the problems are outline its translation to Rmosek is quite easy and they perform fairly well for moderately large problems.
Quantile Regression
The Quantile Regression problem solves the following problem
\[\hat\beta = \underset{\beta \in \mathbb{R}^p}{arg\min}{ \sum_{i=1}^n\ \ \rho_{\tau}\left(y_{i}-x'_{i}\beta\left(\tau\right)\right)}\]which can be written as a linear program. Let \(X\) be a \(n \times p\) matrix of regressors with a constant, and \(y\) an \(n\ \times 1\) vector of the dependent variable. Following Koenker (2005) we can write the quantile problem as a linear problem,
\[\underset{(u,v,\beta)\in\mathbb{R}^{p+2n}}{min }(\tau u +(1-\tau)v)\] \[s.t.\] \[y − X \beta = u − v\] \[u \geq 0\] \[v \geq 0\] \[\beta \in \mathbb{R}^p \]Recall that the primal problem in a linear program can be written as
\[\underset{x}{min } \ \ c'x +c_0\] \[s.t.\] \[l^c \leq Ax \leq u^c\] \[l^x \leq x \leq u^x\]To translate this problem into Rmosek it is useful to make the following correspondences:
\[c = (0_p', \tau e_n', (1-\tau) e_n')'\]where \(e_n\) is an n-vector of ones.
\[x = (\beta',u',v')'\] \[A = [X : I : -I]\]furthermore, note that \(x \in\mathbb{R}^{p+2n}\) and that in this case \(l^c=u^c=y\).
The next step is then to write our own quantile regression function that wraps Rmosek. I call the function qr.mosek and give it as inputs the design X matrix (that should contain a column of ones if the model has a constant) and the dependent variable. Also, takes a variable verb that controls for the “verbosity” of the output’s log. The function begins by getting the relevant dimensions from the data. Then it defines the problem in Mosek. The problem definition starts with an empty list, which I called lo1. The next step is defining the objective goal, which in this case is minimization ("min"). Then we pass the variables following the above correspondences. The last line solves the problem. When defining the problem Rmosek Users Guide becomes a very handy tool, and I follow it closely.
qr.mosek<-function(X,y,tau, verb=1){
n<-length(y) #number of observations
p<-dim(X)[2] # number of parameters of interest
#problem definition in Mosek
lo1<-list() #empty list that contains the LP problem
lo1$sense<-"min" #problem sense
lo1$c<-c(rep(0,p),rep(tau,n),rep((1-tau),n)) #objective coefficients
lo1$A<-Matrix(cbind(X,diag(n),-diag(n)),sparse=TRUE) #constraint matrix
lo1$bc<-rbind(blc=c(y),buc=c(y)) #lower and upper constraint bounds
blx<-c(rep(-Inf,p),rep(0,n),rep(0,n)) #lower parameters bounds
bux<-c(rep(Inf,p),rep(Inf,n),rep(Inf,n)) #upper parameters bounds
lo1$bx<-rbind(blx,bux) #bind the lower and upper paramenter bounds
r<-mosek(lo1, opts = list(verbose = verb)) #call mosek solver
return(r)
}
Mosek uses as default its interior point algorithm and returns an interior point solution and a vertex solution. The primal interior point solution is called itr and can be obtained via $sol$itr$xx. One must be careful when retrieving the solution because we introduced 2n slack variables in the problem. The option verbose on Mosek controls messages priorities, option 1 prints when errors are encountered. Setting it to 0 will silence Mosek completely. The option optimizer can also be specified and allows the user to let Mosek choose the optimizer, or choose an interior point algorithm, or a simplex method on the primal, among others.
The primal form gets “a bit unwieldy” (Koenker and Mizera, 2014) because of these 2n slack variables. However, the problem can be written in the corresponding dual form, which is more convenient for interior point implementations.
\[\underset{d}{max }\ \ y'd\] \[s.t.\] \[X'D=0\] \[d \in [\tau-1, \tau]^n\]A function using Mosek will look like;
qr.mosek.dual<-function(X,y,tau, verb=1){
n<-length(y) #number of observations
p<-dim(X)[2] # number of parameters of interest
#problem definition in Mosek
lo1<-list() #empty list that contains the LP problem
lo1$sense<-"max" #problem sense
lo1$c<-as.vector(y) #objective coefficients
lo1$A<-Matrix(t(X),sparse=TRUE) #constraint matrix
blc<-rep(0,p) #lower constraint bounds
buc<-rep(0,p) #upper constraint bounds
lo1$bc<-rbind(blc,buc) #bind the lower and upper constraint bounds
blx<-c(rep(tau-1,n)) #lower parameters bounds
bux<-c(rep(tau,n)) #upper parameters bounds
lo1$bx<-rbind(blx,bux) #bind the lower and upper parameter bounds
r<-mosek(lo1, opts = list(verbose = verb)) #call mosek solver
return(r)
}
Equivalently, the may be reparametrized as
\[\underset{a}{max }\ \ y'a\] \[s.t.\] \[X'a = (1 − \tau)X'e_n\] \[a \in [0, 1]^n\]and its implementation in Rmosek
qr.mosek.dual.rep<-function(X,y,tau, verb=1){
n<-length(y) #number of observations
p<-dim(X)[2] # number of parameters of interest
#problem definition in Mosek
lo1<-list() #empty list that contains the LP problem
lo1$sense<-"max" #problem sense
lo1$c<-as.vector(y) #objective coefficients
lo1$A<-Matrix(t(X),sparse=TRUE) #constraint matrix
e<-matrix(1,ncol=1,nrow=n) #vector of ones
blc<-(1-tau)*c(crossprod(X,e)) #lower constraint bounds
buc<-(1-tau)*c(crossprod(X,e)) #upper constraint bounds
lo1$bc<-rbind(blc,buc) #bind the lower and upper constraint bounds
blx<-c(rep(0,n)) #lower parameters bounds
bux<-c(rep(1,n)) #upper parameters bounds
lo1$bx<-rbind(blx,bux) #bind the lower and upper parameter bounds
r<-mosek(lo1, opts = list(verbose = verb)) #call mosek solver
return(r)
}
Again, the solution to the interior point method is accessed via $sol$itr. In these cases, we must be careful because we want to retrieve the solution to the dual variables.
OLS as a Quadratic Program
Now I turn to our more familiar Ordinary Least Squares. It solves
\[\hat \beta = \underset{ \beta \in \mathbb{R}^p}{arg\min}{ \sum \_{i=1}^n\ \ \left(y\_{i}-x'\_{i}\beta\right)^2}\]with a little use of algebra, we can write this problem as a Quadratic Program
\[\hat\beta = \underset{\beta \in \mathbb{R}^p}{arg\min}{(-2\beta'X'y+ \beta'X'X\beta)}\]recall that a general form of a Quadratic program is \(x = \underset{x \in \mathbb{R}^p}{arg\min}{( \frac{1}{2}xQx-x'c)}\)
\[s.t.\] \[Ax = c\]so, making the appropriate correspondences we have the Ordinary Least Squares problem. Note that the OLS case, is unconstrained, which will become handy when specifying the problem in the solver.
To implement the problem in Rmosek I proceed as before. First, I create a function that wraps the definition of the optimization problem and Mosek’s optimizer. The function is called solve.ols and has the same inputs and options as before. The first half of the function is devoted to setting the correspondences between OLS and the Quadratic Program, the second half we simple follow Rmosek Users Guide to define the minimization problem.
solve.ols<-function(X,y, verb=1){
p<-dim(X)[2] # number of parameters of interest
#correspondence between OLS and the Quadratic Program
xx<-crossprod(X) # X'X=Q variable in the Quadratic program
c<--crossprod(X,y) # X'y=c variable in the Quadratic program
xx2<-xx
xx2[upper.tri(xx)]<-0 #mosek needs Q to be triangular
idx <- which(xx2 != 0, arr.ind=TRUE) #index of the nonzero elements of Q
#problem definition in Mosek
qo1<-list() #empty list that contains the QP problem
qo1$sense<-"min" #problem sense
qo1$c<-as.vector(c) #objective coefficients
qo1$qobj<-list(i = idx[,1],
j = idx[,2],
v = xx2[idx] ) #the Q matrix is imputed by the row indexes i, the col indexes j and the values v that define the Q matrix
qo1$A<-Matrix(rep(0,p), nrow=1,byrow=TRUE,sparse=TRUE) #constrain matrix A is a null matrix in this case
qo1$bc<-rbind(blc=-Inf, buc= Inf) #constraint bounds
qo1$bx<-rbind(blx=rep(-Inf,p), bux = rep(Inf,p)) #parameter bounds
r<-mosek(qo1, opts = list(verbose = verb)) #call mosek solver
return(r)
}
Applications
Simulation
We are now ready to test our function. I set a mock problem where the independent variable does not have an effect on the conditional mean but the effect is on the variance.
set.seed(1212)
x<-rep(1:20,each=500)
n<-length(x)
cons<-rep(1,n)
X<-cbind(cons,x)
y<-rnorm(n,mean=0,sd=x^.8)
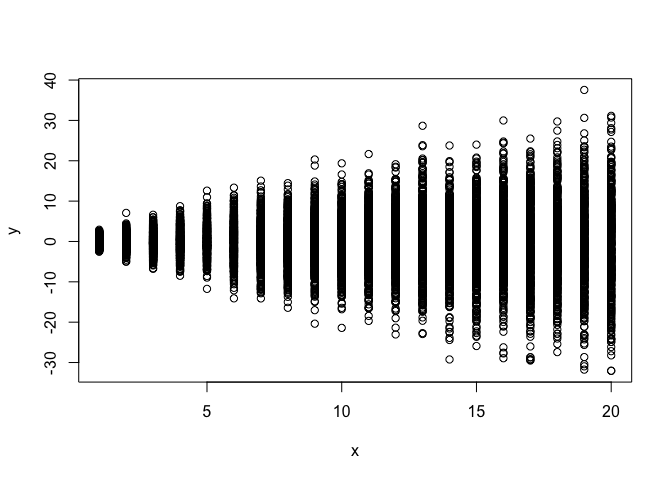
Plotting the simulation clearly shows how that the effect of the independent variable on the mean is zero but the variance increases with it.
plot(x,y)
First, once we have installed Rmosek, we call it
require(Rmosek, quietly = T)
Suppose we want to assess the effect on the median (τ = .5)
tau<-0.50
z<-qr.mosek(X,y,tau=tau)
head(z$sol$itr$xx,dim(X)[2])
[1] -0.039657474 0.008174528
The parameter results are located under $sol$itr$xx. Note that the parameters of interest are only the first p parameters. The solution includes p × 2n results, p parameters and 2n slack variables, but only the first p are of interest. As expected the effect on the median is null.
Suppose now that we want to assess the effect on the 90t**h quantile, where we should expect a positive effect of the independent variable.
tau<-0.90
z<-qr.mosek(X,y,tau=tau)
head(z$sol$itr$xx,dim(X)[2])
[1] 1.0165950 0.6772688
To compare Mosek performance we choose quantreg package (Koenker, 2016), which is the most used package to solve this type of problems in R. The default solver in the quantreg package is the function rq.fit.br. This function calls algorithm of Koenker and d’Orey (Koenker, 2016).
require(quantreg)
rq.fit.br(X,y,tau=tau)$coefficients
cons x
1.0165950 0.6772688
Results are numerically identical under Mosek and the quantreg package. More interesting however is testing how Mosek solver compares in computation time to the quantreg package default. I test then the primal, the dual, and the reparametrized dual, against the function rq.fit.br
microbenchmark::microbenchmark(
qr.mosek(X,y,tau=tau),
qr.mosek.dual(X,y,tau=tau),
qr.mosek.dual.rep(X,y,tau=tau),
rq.fit.br(X,y,tau=tau)
)
Unit: milliseconds
expr min lq mean
qr.mosek(X, y, tau = tau) 2866.959432 3132.532709 3238.346004
qr.mosek.dual(X, y, tau = tau) 93.354619 95.710071 98.888875
qr.mosek.dual.rep(X, y, tau = tau) 93.863603 95.716660 98.375217
rq.fit.br(X, y, tau = tau) 8.280732 8.459964 8.892775
median uq max neval
3172.331852 3355.718077 3809.76471 100
96.661428 99.848480 128.10002 100
96.848799 99.052075 120.14091 100
8.582349 8.987302 12.99779 100
It’s clear now how unwieldy the primal problem. It takes considerably more time than the dual formulations or the rq.fit.br function. And the dual formulations in Mosek are considerable slower than the rq.fit.br function.
Next, I examine how the OLS solver works. First, I call the function I constructed before
solve.ols(X,y)$sol$itr$xx
[1] 0.020485604 -0.005660287
and I compare it to the traditional lm function in the base package
summary(lm(y ~ X-1))$coef[,1]
Xcons Xx
0.020485604 -0.005660287
note the −1 in the lm line because the X already includes a constant in X. Once again numerically they are identical. Comparing times, I find that Mosek is quite considerably faster than the base lm. I should test however this with more complex problems.
microbenchmark::microbenchmark(
lm(y ~ X-1),
solve.ols(X,y)
)
Unit: milliseconds
expr min lq mean median uq
lm(y ~ X - 1) 6.063136 9.518182 10.313522 9.809023 10.261577
solve.ols(X, y) 1.007566 1.164319 2.313304 1.426241 1.547576
max neval
60.70589 100
82.68025 100
Replication: The Wage Distribution
Next, I turn to an application taken from Mostly Harmless Econometrics (Angrist & Pischke, 2008). The application replicates Angrist, et al (2006) Quantile Regression under Misspecification, with an Application to the U.S. Wage Structure paper. All the relevant files to replicate the paper are publicly available on Angrist’s Data Archive
Files are in Stata format, so I use the foreign package to read the data set corresponding to the 2000 census. The data set is quite large, it contains 97397 observations and 5 variables: the logarithm of wage, education, race, experience and experience squared.
require(foreign)
Loading required package: foreign
dta<-read.dta( "~/Data/census00.dta")
y<-dta$logwk
X<-cbind(rep(1,length(y)),dta$educ,dta$black,dta$exper,dta$exper2)
dim(X)
[1] 97397 5
We focus here on the dual problem, and focus only on the returns to schooling for five quantiles: .10, .25, .50, .75 and .90, and also the Mean Estimate using OLS
-qr.mosek.dual(X,y,tau=.1)$sol$itr$suc[2]
[1] 0.09090798
-qr.mosek.dual(X,y,tau=.25)$sol$itr$suc[2]
[1] 0.1033592
-qr.mosek.dual(X,y,tau=.5)$sol$itr$suc[2]
[1] 0.1110223
-qr.mosek.dual(X,y,tau=.75)$sol$itr$suc[2]
[1] 0.1215066
-qr.mosek.dual(X,y,tau=.9)$sol$itr$suc[2]
[1] 0.1549263
solve.ols(X,y)$sol$itr$xx[2]
[1] 0.1148
It interesting how the average return is about 11 but when we focus on the quantiles a different pattern emerges. The mean and median returns are quite similar but larger returns to schooling appear as we move to the upper quantiles. I could not end this incursion into Mosek without comparing computation times for the application.
tau<-0.5
microbenchmark::microbenchmark(
qr.mosek.dual(X,y,tau=tau),
rq.fit.br(X,y,tau=tau)
)
Unit: milliseconds
expr min lq mean median
qr.mosek.dual(X, y, tau = tau) 420.2002 434.9739 473.0457 456.4372
rq.fit.br(X, y, tau = tau) 4642.0985 4761.6424 5034.9789 5052.8138
uq max neval
472.2065 889.6079 100
5226.3060 5975.6663 100
Mosek now turns to be considerable faster than rq. Thus, for a moderately large problem and using the dual formulation of the quantile program Mosek performs quite well.
To finish, those interested in convex optimization with R I would recommend reading the paper by Koenker and Mizera (2014) Convex Optimization in R.
Comments and suggestions are always welcomed. You can send them to srmntbr2 at illinois.edu.
References and Further Readings
Angrist, J., Chernozhukov, V., & Fernández‐Val, I. (2006). Quantile regression under misspecification, with an application to the US wage structure. Econometrica, 74(2), 539-563.
Angrist, J. D., & Pischke, J. S. (2008). Mostly harmless econometrics: An empiricist’s companion. Princeton university press.
Friberg HA (2014). Rmosek: The R-to-MOSEK Optimization Interface. R package version 1.2.5.1, URL http://CRAN.R-project.org/package=Rmosek.
Koenker, R. (2005). Quantile regression. No. 38. Cambridge university press.
Koenker, R. (2016). quantreg: QuantileRegression. R package version 5.29. https://CRAN.R-project.org/package=quantreg
Koenker, R., & Hallock, K. (2001). Quantile regression: An introduction. Journal of Economic Perspectives, 15(4), 43-56.
Koenker, R., & Mizera, I (2014). “Convex optimization in R.” Journal of Statistical Software 60, no. 5: 1-23.
MOSEK ApS, Denmark (2011). The MOSEK Optimization Tools Manual. Version 6.0, http://www.mosek.com/.
Ignacio
Sarmiento Barbieri
University of Los Andes
- srmntbr2 (at) illinois.edu
- ignaciomsarmiento (at) gmail.com
- ignaciomsarmiento
Blogs/Links
These are blogs/sites I frequently visit